Atividades de Matemática para o 8 ano A e B

E. E. PROFª MARIA CINTRA NUNES ROCHA		Turma:  → 8 ano A e B			Data:   →	___/___/___	Valor: 0 → 10
		Disciplina:		Matemática	Professor:	Ana Karina	Nota:
Atividades remotas - Distanciamento Social COVID-19	Critério		Cumprimento de tarefas individuais
	Habilidade
	Competência		Resolução de problemas
Nome:						Errando todas  🡪  0

“RESPOSTAS FINAIS A CANETA” / “DEMONSTRAR RESOLUÇÔES! ORGANIZADAMENTE! ”

Realize as atividades pedidas aqui, todas em seu caderno! Sempre respeitando a sequência em que elas foram propostas! (1, 2, 3, 4, 5, ...). Para auxiliar o seu estudo você deve utilizar o livro didático de Matemática! Assim como qualquer outro recurso que você tenha disponível!

Atenção: Leia atentamente as orientações e atividades deste documento.

Habilidades e competências:

EF07MA05 – Ler, interpretar e resolver um mesmo problema utilizando

diferentes algoritmos. Fração e seus significados: como parte de inteiros,

resultado da divisão, razão (porcentagem, razão entre as partes de um todo e

probabilidade) e operador.

EF07MA02 – Resolver e elaborar situações-problema que envolvam

porcentagem, como os que lidam com acréscimos e decréscimos simples,

utilizando estratégias pessoais, cálculo mental e calculadora no contexto de

educação financeira, entre outros. Cálculo de porcentagem e acréscimos e

decréscimos simples.

EF08MA04 – Resolver e elaborar situações-problema, envolvendo cálculo de

porcentagens, incluindo o uso de tecnologias digitais. Porcentagens.

Observe os exemplos de situações-problemas a seguir e responda os

exercícios em seu caderno. Não se esqueça de registrar a data no topo da

folha em que você apresentará as soluções.

1º exemplo: O que é Probabilidade?

Está associado a chance de determinado evento acontecer. Encontramos a

probabilidade realizando a divisão entre o número de eventos favoráveis pelo

total de resultados possíveis.

Ex: Em uma gaveta há camisas das cores azul, amarela, verde, vermelha e lilás.

Sem olhar, qual a probabilidade de você pegar a camisa verde?

Observe que temos apenas (1) caso favorável, que é pegar a camisa verde,

dentre (5) casos possíveis, que são todas as cores das camisas, ficando assim:

Para transformar a razão 1/5 em porcentagem, basta multiplicar o numerador (1) por 100 e dividir o resultado pelo denominador (5), desta forma:

Exercício 1. Em uma sala há 12 meninos e 18 meninas. Escolhendo uma pessoa

ao acaso, qual a probabilidade de:

a) ser um menino?

b) ser uma menina?

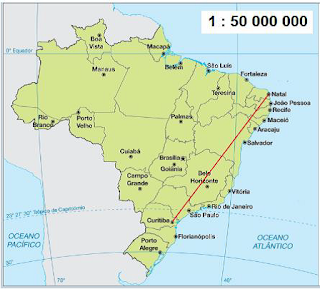
2º Exemplo: Escala, um tipo de razão.

A Escala é um tipo de razão encontrada, principalmente, em mapas e

maquetes. Veja o exemplo:

No exemplo, a escala dada é de 1 : 50 000 000, ou seja, uma (1) unidade de

medida no mapa equivale a 50 000 000 dessa mesma unidade na superfície

real, que no caso é a superfície do nosso país. Sendo assim, um centímetro

do mapa equivale a 50 000 000 de centímetros, ou 500 quilômetros no nosso

país.

Se medirmos com uma régua, o ponto de Curitiba ao ponto de Natal, e

encontrarmos 5,3 cm, podemos determinar a distância real entre essas duas

capitais, fazendo:

Exercício 2: Utilizando as informações do exemplo anterior, determine:

a) a distância real entre duas cidades que estão a 3 cm uma da outra no

mapa.

b) a medida no mapa entre Brasília e São Paulo, sabendo que a distância

real é de aproximadamente 1000 km.

3º exemplo: Porcentagem, fração de alguma quantidade.

A porcentagem é uma fração de algum valor numérico, por exemplo:

Se quisermos obter quanto é 20% de R$ 600,00, basta fazer;

Como você deve ter percebido no esquema, se quisermos obter 20% de 600,

basta efetuar os cálculos; divida 600 por 100 e multiplica o resultado obtido por

200, obtendo 120. Assim, 20% de R$ 600,00 é R$ 120,00.

Exercício 3: Uma bicicleta custa R$ 400,00 na compra à vista. Se na compra a

prazo, o preço final sofre um acréscimo de 15%, quanto vou pagar pela bicicleta em uma compra a prazo?

4º exemplo: Radiciação e alguns cálculos extras.

Sabemos que quando queremos, por exemplo, calcular a raiz quadrada* de 25,

que se representa por √25 2 = √25 , basta encontrar um número que

multiplicado por ele mesmo dê 25, que no caso é 5, pois 5x5 = 25. Logo √25 2 =

√25 = 5, note que, para as raízes de índice 2 não é necessário escrevê-lo na

notação, ou seja, se a raiz estiver “sem índice” subentende-se que o índice é 2.

De maneira semelhante, podemos encontrar a raiz cúbica** de um número, por

exemplo, √64 3 = 4, pois 4 x 4 x 4 = 64. Perceba que na raiz cúbica,

encontramos o resultado quando obtemos o número que multiplicado por ele

mesmo, por três vezes, resulta no radicando e assim sucessivamente.

Se quisermos calcular √81%, temos que rescrever 81% como 81/100, ficando:

Exercício 4: Determine os valores das raízes a seguir.

a) √121 =

b) √27 3 =

c) √16 4 =

d) √9% =

Faça o que você conseguir! Se ficar duvidas as anote no seu caderno e em uma próxima aula nos as retiramos!